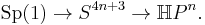Quaternionic projective space

In mathematics, quaternionic projective space is an extension of the ideas of real projective space and complex projective space, to the case where coordinates lie in the ring of quaternions H. Quaternionic projective space of dimension n is usually denoted by

HPⁿ

and is a closed manifold of (real) dimension 4n. It is a homogeneous space for a Lie group action, in more than one way.

1 In coordinates
2 Projective line
3 Infinite-dimensional quaternionic projective space
4 Quaternionic projective plane
5 References
6 Further reading

In coordinates

Its direct construction is as a special case of the projective space over a division algebra. The homogeneous coordinates of a point can be written

[q₀:q₁: ... :q_n]

where the q_i are quaternions, not all zero. Two sets of coordinates represent the same point if they are 'proportional' by a left multiplication by a non-zero quaternion c; that is, we identify all the

[cq₀:cq₁: ... :cq_n].

In the language of group actions, HPⁿ is the orbit space of Hⁿ⁺¹-(0, ..., 0) by the action of H*, the multiplicative group of non-zero quaternions. By first projecting onto the unit sphere inside Hⁿ⁺¹ one may also regard HPⁿ as the orbit space of S⁴ⁿ⁺³ by the action of Sp(1), the group of unit quaternions.^[1] The sphere S⁴ⁿ⁺³ then becomes a principal Sp(1)-bundle over HPⁿ:

$\mathrm{Sp}(1) \to S^{4n%2B3} \to \mathbb HP^n.$

There is also a construction of HPⁿ by means of two-dimensional complex subspaces of C²ⁿ, meaning that HPⁿ lies inside a complex Grassmannian.

Projective line

The one-dimensional projective space over H is called the "projective line" in generalization of the complex projective line. For example, it was used (implicitly) in 1947 by P. G. Gormley to extend the Möbius group to the quaternion context with "linear fractional transformations". See inversive ring geometry for the uses of the projective line of the arbitrary ring.

From the topological point of view the quaternionic projective line is the 4-sphere, and in fact these are diffeomorphic manifolds. The fibration mentioned previously is from the 7-sphere, and is an example of a Hopf fibration.

Infinite-dimensional quaternionic projective space

The space 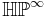$\mathbb{HP}^{\infty}$ is the classifying space BS³; and, rationally (i.e. after localisation of a space it is an Eilenberg–Maclane space K(Z,4) (cf. the example K(Z,2)). See rational homotopy theory.

Quaternionic projective plane

The 8-dimensional HP² has a circle action, by the group of complex scalars of absolute value 1 acting on the other side (so on the right, as the convention for the action of c above is on the left). Therefore the quotient manifold

HP²/U(1)

may be taken, writing U(1) for the circle group. It has been shown that this quotient is the 7-sphere, a result of Vladimir Arnold from 1996, later rediscovered by Edward Witten and Michael Atiyah.

References

^ Gregory L. Naber, Topology, geometry, and gauge fields: foundations (1997), p. 50.